本研究針對具有異向性降伏面、拉壓不對稱降伏點的非線性等向、走動硬軟化彈塑性模式,建立其數值積分法。相較於一般的塑性積分法,其必須使用預測/修正法來將計算出的應力迭代拉回降伏面上,本研究藉由模式的內在對稱性,獲得可計算出自動滿足降伏條件的應力算法,故此方法被命名為免映射法(return-free integration)。本研究更進一步,在數值驗證方面,探討了免映射法的一致性誤差(consistency error)(圖一)、收斂性分析(convergence analysis)(圖二)和等誤差圖(iso-error map)(圖三)。並結合不同加載路徑的分析(圖四)和加入初始條件下的狀況,進行了全面的驗證。並且,在計算效率上,通過與傳統映射法(return-mapping integration)的計算時間對比(圖五),清晰地展示了所提出免映射積分法,在保持高精度的同時也具有更優秀的計算效率。整體而言,我們展示了免映射塑性積分法是一個穩定、優異與可靠的塑性積分法。(土木系劉立偉教授提供)
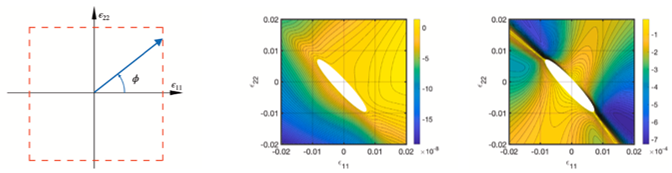
圖一 (a) ϵ11- ϵ22控制路徑。(b) return-free積分法的一致性誤差圖。(c) RK4積分法的一致性誤差圖。
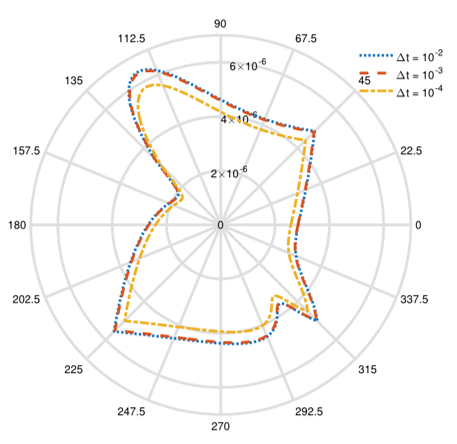
圖二 對於等向運動硬化混合模型在不同時間步長的平均誤差。
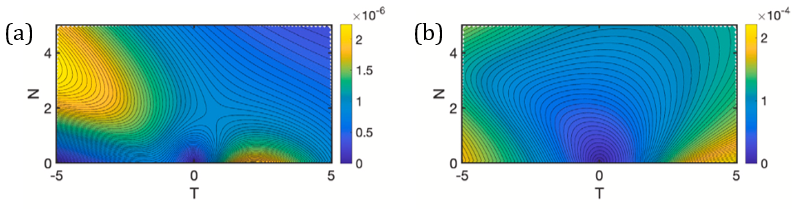
圖三 (a) 對於等向運動硬化混合模型的徑向誤差圖。(b) 對於等向運動硬化混合模型的角度誤差圖。
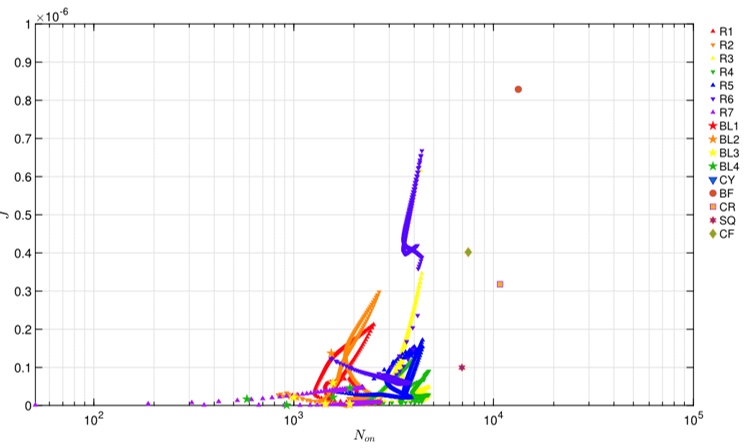
圖四 對於等向運動硬化混合模型在16種加載路徑下的 J-Non 圖。
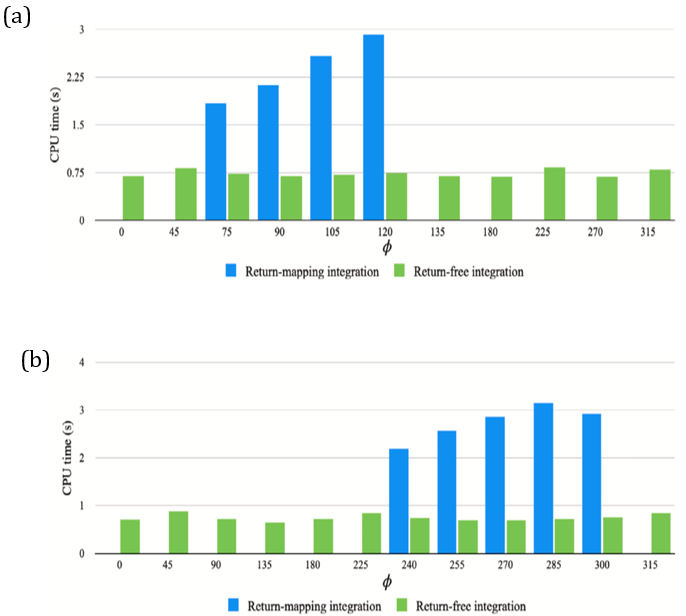
圖五 (a) 無初始條件下的CPU運算時間對比圖。(b) 初始條件為σ11=50MPa及σ22= -75MPa下的CPU運算時間對比圖(在映射法中,在某些角度的路徑,無法獲得滿足收斂條件之結果,因此沒有獲得可呈現的時間。)。