https://doi.org/10.1109/TAC.2024.3396775
多變數系統需同時滿足多項性能目標,因此控制器設計往往需要在多個系統性能之間進行折衷。例如,光學桌系統需要在有限的減振行程內,保持桌面穩定,應對來自地面擾動及機器震動的影響;而汽車懸吊系統則必須處理來自地面的擾動及車身的作用力,兼顧舒適性與操控性。這些多輸入多輸出系統之間的性能調整常常息息相關,一個微小的變動可能會影響整體系統的表現。因此,如何在確保特定傳輸路徑性能的同時,進行最佳化設計,變得尤為重要。為此,本論文提出了一種創新的控制理論–混和擾動響應解偶 (Hybrid Disturbance Responses Decoupling, HDRD),可以對多變數系統提供解偶控制,實現獨立控制器設計,並同時提升系統性能。
本人之前提出了擾動響應分解(Disturbance Responses Decoupling, DRD)理論 [1],可以在保持特定傳輸路徑不變的前提下,改善其他轉移函數的性能,從而實現獨立控制器設計的目標。數值範例如圖一所示,對於一個雙輸入雙輸出系統,我們可以設計四個控制器,分別使四個閉迴路轉移函數保持與開迴路一致(即保持原有性能),同時提升其他傳輸路徑的性能。DRD 理論已被成功應用於車輛懸吊系統 [2] 和光學桌減振系統 [3],並取得了顯著的成果。然而,儘管 DRD 理論能在保持特定傳輸路徑轉移函數不變的條件下改善其他轉移函數的性能,它仍無法同時提升多個轉移函數的性能。例如,在圖2中,該理論無法實現四個轉移函數的獨立控制,這限制了其進一步發展的潛力。
為了解決上述問題,我們提出了 DRD 理論的互補理論–混合擾動響應分解(HDRD) [4]。該理論可以針對每個傳輸路徑設計控制器,調整其轉移函數,並結合所有控制器,全面提升系統性能。HDRD 控制架構如圖二所示,數值範例則呈現在圖三中。在這一架構下,我們可以獨立設計四個輸入響應輸出分解(input-output disturbance response decoupling, IODRD)控制器,分別控制特定的轉移函數,同時保持其他傳輸路徑不變。最終,通過圖二所示的 HDRD架構整合這四個控制器,達到圖三(e) 中的結果。HDRD 理論使我們能夠針對多變數系統的每個傳輸路徑設計獨立的控制器,並利用 HDRD 架構將所有設計結果整合在一起,從而同時滿足各個轉移函數的控制需求,且各控制器之間不會相互干擾。(機械系王富正教授提供)
Reference:
[1] M. C. Smith and F. C. Wang, "Controller parameterization for disturbance response decoupling: application to vehicle active suspension control," IEEE Trans. Control Syst. Technol., vol. 10, no. 3, pp. 393-407, 2002, doi: 10.1109/87.998029.
[2] F. C. Wang and M. C. Smith, "Disturbance response decoupling and achievable performance with application to vehicle active suspension," Int. J. Control, vol. 75, no. 12, pp. 946-953, 2002.
[3] F. C. Wang, C. H. Yu, J. Tsai, and S. H. Yang, "Decoupled robust vibration control of an optical table," J. Vib. Control, vol. 20, pp. 38–50, 2012, doi: 10.1177/1077546312461369.
[4] F. C. Wang and C. H. Lee, “Hybrid Disturbance Response Decoupling for Multivariable Systems”, IEEE Trans. Auto. Control, Vol. 69, no.10, pp. 7277–7284. https://doi.org/10.1109/TAC.2024.3396775
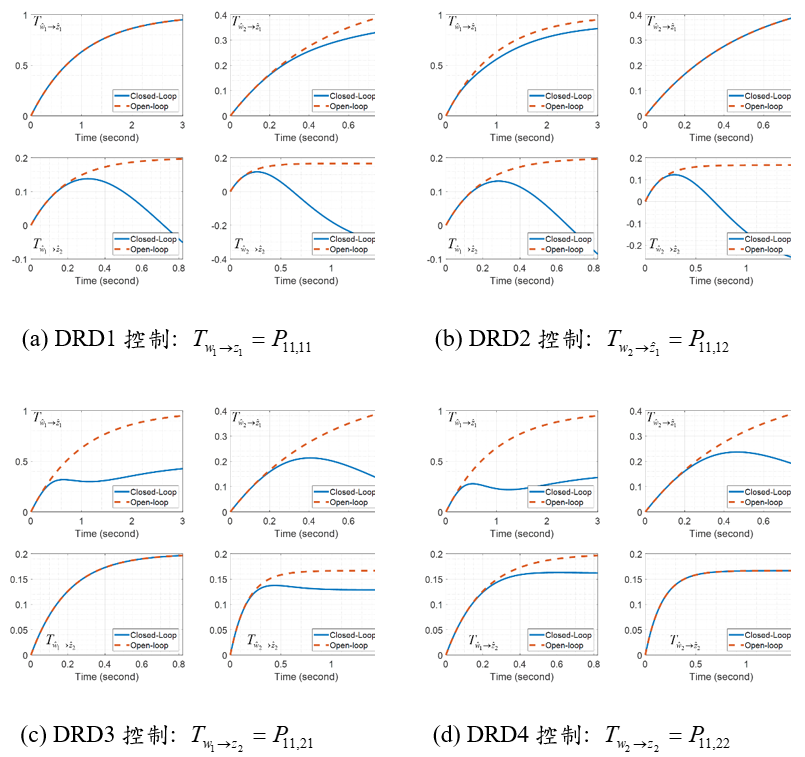
圖一、利用DRD控制之系統響應。
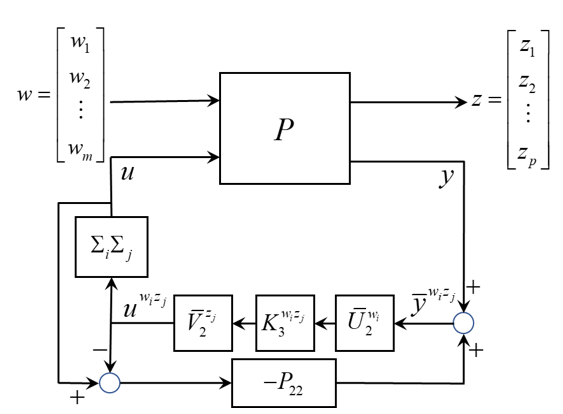
圖二、混合擾動響應分解 (HDRD) 控制架構。
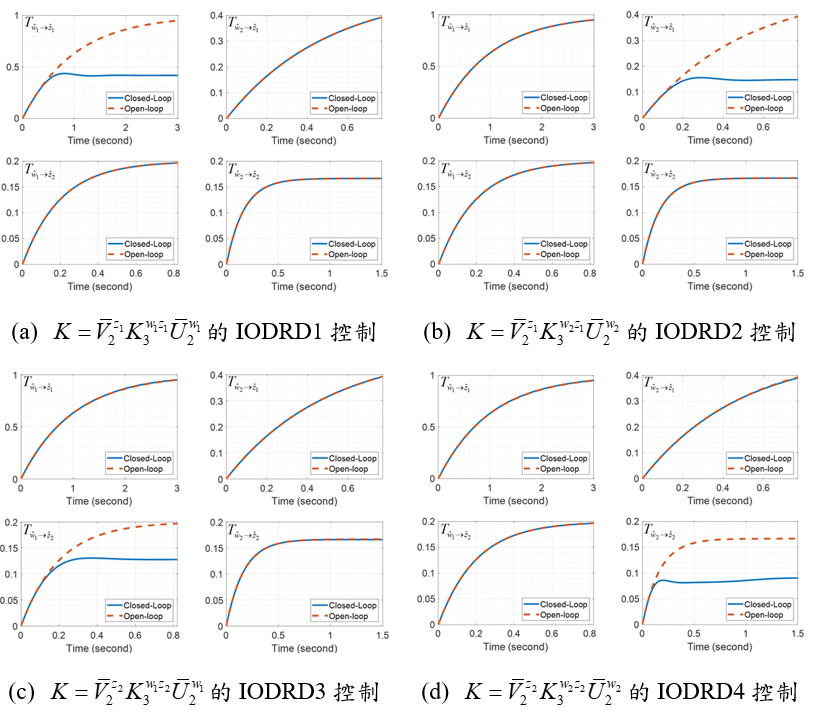
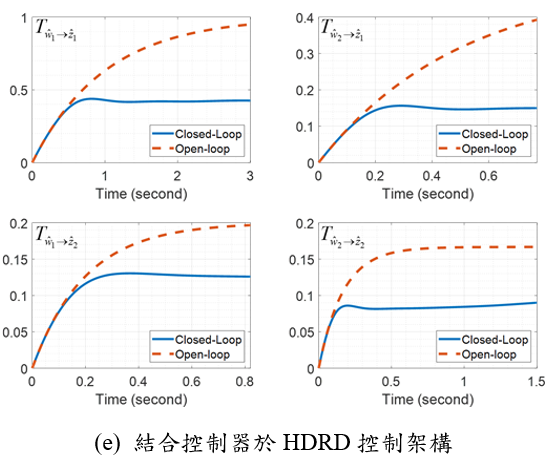
圖三、利用IODRD與HDRD控制之系統步階響應。