如圖一,光學振鏡(Galvanometer)是加法製造、輪廓測量以及醫學影像中光束導引的關鍵元件。在這些應用中,儀器設備的品質仰賴於光學振鏡的精確運動控制,以追蹤或抑制窄帶信號。根據內部模型原理(Internal Model Principle),這可以通過將參考或干擾信號的動態模型納入迴授路徑來實現。本文提出了一種基於數值穩健全通濾波器的創新內部模型原理控制器。其主要概念是將控制器設計轉化為基於全通濾波器(all-pass filter)的相位響應設計問題。針對所提方法,內部模型的目標頻率可以任意選擇而不犧牲性能。此外,此方法生成較低階的控制器,並對量化效應具有良好的強韌性。當與頻率估測演算法和自適應濾波器結合時,可以直接應用於未知和時變干擾的抑制。通過分析、模擬和實驗,將本文所提方法與傳統方法進行比較並展示其優點。(機械系李宇修教授提供)
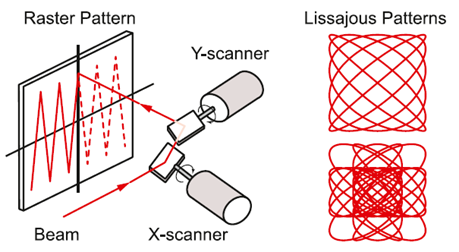
圖一、光學振鏡系統用於雷射光導引示意圖。藉由X與Y兩軸掃描器的協同運動建構在平面上不同的掃描圖譜。
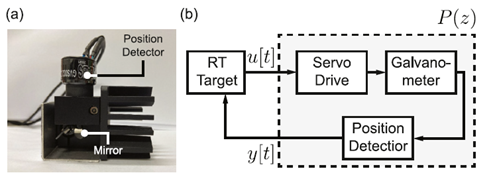
圖二、(a)受控之光學振鏡硬體,(b)機電系統架構。
圖二為用於實驗的硬體和機電系統連接架構,主要的控制演算法建置在實時目標電腦(real-time target PC),由振鏡角度 y[t] 的迴授決定控制訊號 u[t] 。根據內部模型原理,追蹤或抑制諧波與週期信號的控制器可使用圖三中的Cimp表達,具體包含一帶通(band-pass)頻率選擇器 L 、相位補償器 Φ 、系統 P 之逆動態 F 及其延遲補償 Z-m。

圖三、(a)嵌入式內部模型原理控制器架構,(b)內部模型原理控制器 Cimp 之內部結構。
本文的創新之處在於利用全通式濾波器的彈性與數值穩定性來實作頻率選擇器 L 與相位補償器 Φ ,藉此獲得更優越的性能表現。如圖四,藉由設計不同頻率下的相位響應,透過簡單的幾何運算便能得到派生的帶通與陷波濾波器。注意圖三中所有方塊除系統 P 之逆動態 F 外都可以使用全通式濾波器的相位設計得到。
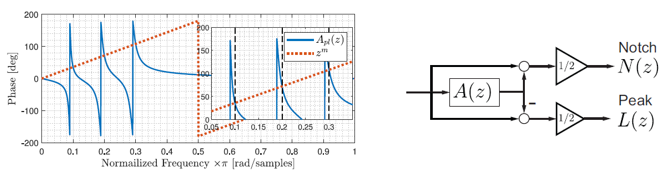
圖四、左:全通式濾波器的相位響應,可以藉由濾波器設計令其在指定頻率有預期的相位表現;右:全通式濾波器 A(z) 的相位特性可用以建構指定頻率的陷波 N(z) 與帶通濾波器 L(z) 。
圖五具體比較使用全通式濾波器(all-pass filter,AP)與傳統梳狀濾波器(comb filter,CF)用於陷波濾波的性能與受數值運算量化效應的影響,可以看出全通式濾波器串接有最數值強韌的表現。
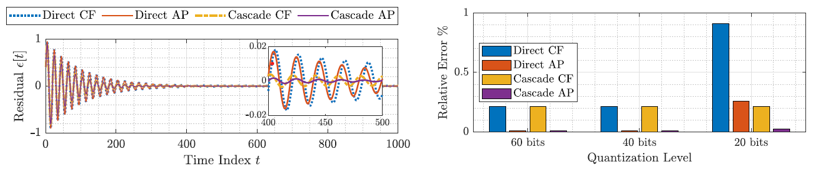
圖五、左:比較全通式濾波器與傳統梳狀濾波器用於陷波濾波的性能;右:量化誤差對效能影響。
以全通式濾波器、梳狀濾波器與重複控制(repetitive control,RC)建置內部模型原理控制器於追蹤100 Hz與350 Hz的諧波訊號,從圖六中敏感度的比較可以看出基於全通式濾波器的做法有最好的低敏表現,且對原始敏感度的影響相對較小。實作追蹤混成諧波訊號可看出本文所提倡的方法有較佳的時間收斂性和穩態誤差。
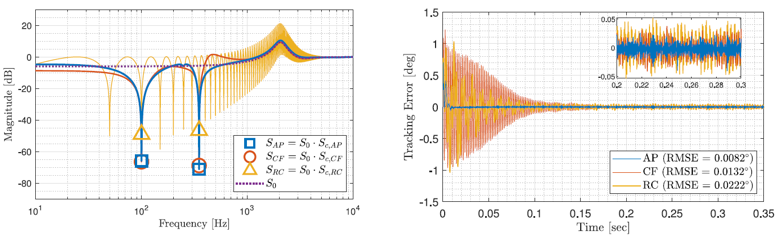
圖六、左:全通式濾波器、梳狀濾波器與重複控制和原始系統敏感度比較;右:追蹤100 Hz與350 Hz的諧波訊號之追蹤誤差。
若考慮應用場合為諧波成分未知的擾動抑制,則可以結合頻率估測和適應性控制,藉由線上偵測的諧波成分實時建構內部模型達成更為彈性的應用。圖七為使用該進階架構在有雙頻道擾動影響系統的時域與時頻訊號圖,可以看出在時變內部模型控制器的作用下干擾被有效抑制,兩個變化的諧波成分都被消弭至接近雜訊的數量級大小。
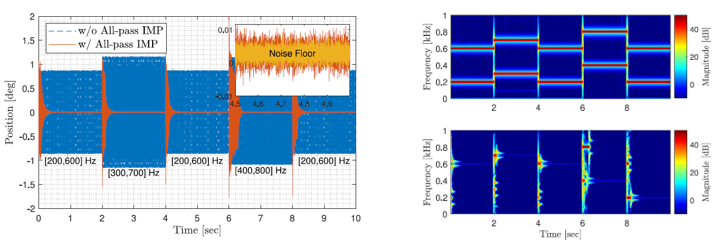
圖七、左:抑制雙頻諧波擾動的時域訊號圖;右:抑制雙頻諧波擾動的時頻分析,上為未使用內部模型控制器時,下為使用該控制器後。