高分子系統的相分離過程在實務應用上是一項重要現象,其速度與程度將直接影響材料的最終性質。然而,使用傳統的電腦模擬預測此過程時,需解決高階非線性微分方程,計算繁瑣且耗時。因此,本團隊開發了一種數據驅動的時空模型(ST模型)以有效捕捉相分離過程中空間與時間的特徵相關性,稱為L-MAU。此模型可以彈性結合降維方法,以加速相分離過程的求解與預測(如圖一所示)。
我們將預測步驟分為三個階段。第一階段透過不同技術降低高維度相分離過程的數據維度,然後將降維後的資訊輸入第二階段的核心模型 L-MAU。最後,在第三階段,透過升維技術還原高維度的相分離圖形。為了綜合呈現L-MAU的預測能力,本研究比較了三種不同的降維方法:(1) 以主成分分析(PCA)處理相分離的兩點相關函數(two-point correlation function;Grad (r)),作為模型的低維輸入;(2) 利用自動編碼器(Autoencoder)學習並壓縮高維度特徵,同時佐以主成分分析來節省自動編碼器的計算資源;(3) 在自動編碼器的損失函數(loss function)中加入物理限制,以確保降維後的特徵能保留關鍵物理特徵。圖二與圖三展示了四種不同類型的相分離過程,並比較了只使用主成分分析與結合物理條件限制自動編碼器後的訓練效果。結果顯示,具有物理限制的自動編碼器能在降維與升維過程中最大程度地保留細微的結構資訊。在這些比較中,我們也設計不同的誤差指標(ARE比較結構特徵長度的誤差;AIE比較局部濃度分布的誤差)來定量預測的準確度。
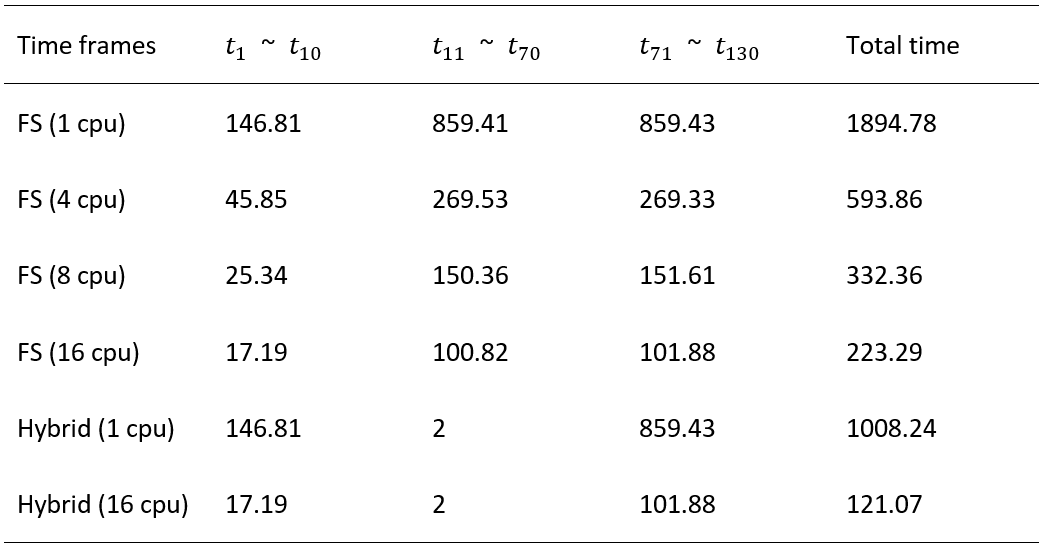
鑑於資訊流失無法完全避免,本研究進一步將降維預測與傳統數值方法結合,並將預測結果作為後續數值計算的起始條件,以期能用更穩定的結構初始條件來提升數值模擬的穩健性。圖四與表一分別展示了純數值解與此混合方法(Hybrid)的結構預測與計算效率比較。此部分的結果顯示,混合方法能有效控制誤差,並藉由L-MAU模型的預處理加速數值計算。此外,此方法還能避免數值方法在初期相分離時,由於結構瑣碎與不規律所造成的不穩定性,使後續數值模擬能夠採用較大的時間步伐,提高計算效率。(化工系游琇伃教授提供)
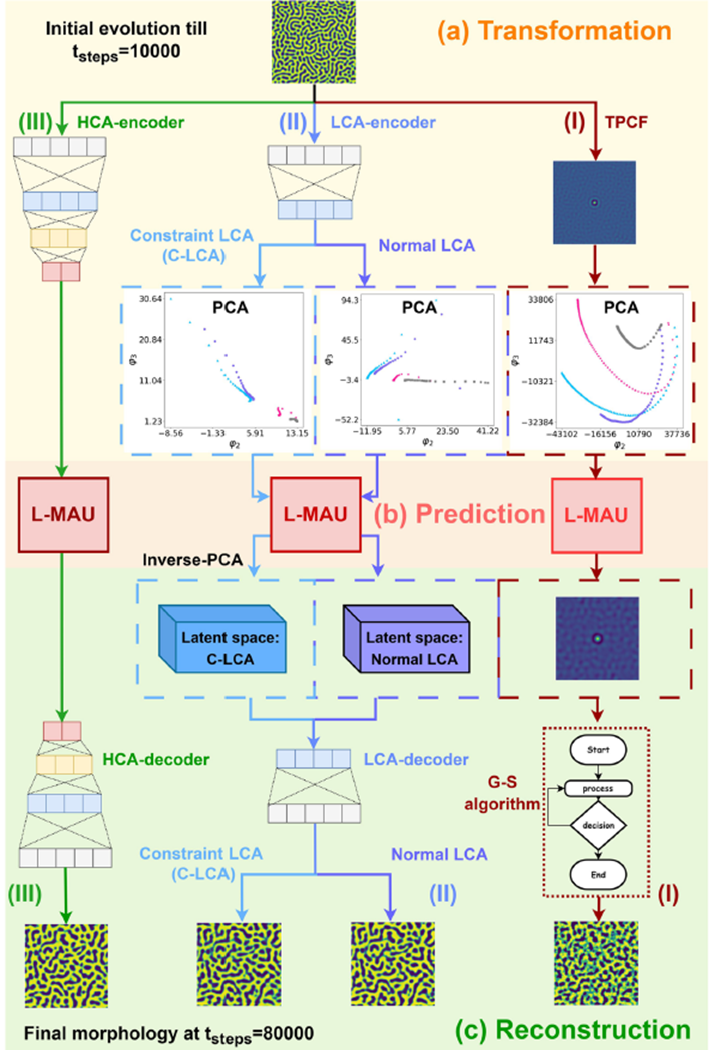
圖一、時間序列模型L-MAU輔以低維度方法預測高分子溶液的相分離結構變化。此圖呈現預測過程的三大階段:降維(Transformation)、預測(Prediction)、還原(Reconstruction)。
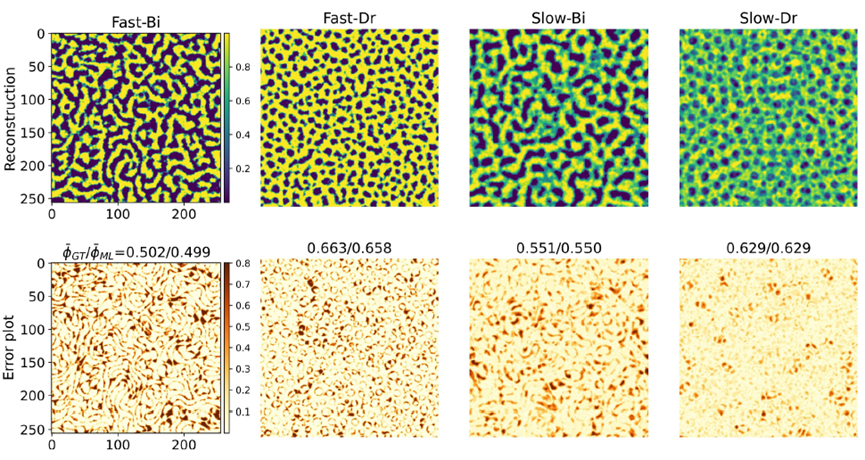
圖二、兩點相關函數結合主成分分析之結構還原結果。
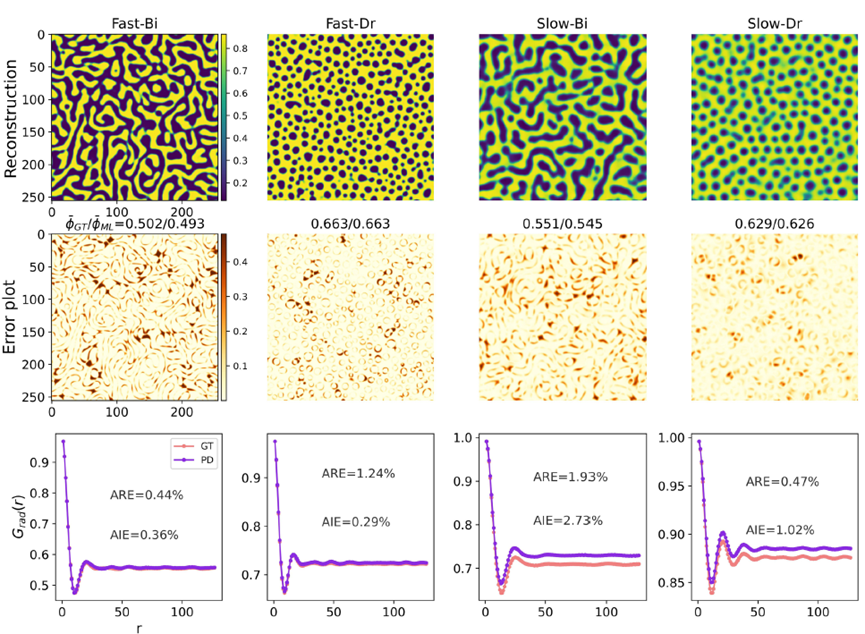
圖三、整合物理條件限制下自動編碼器結合主成分分析之還原結果。
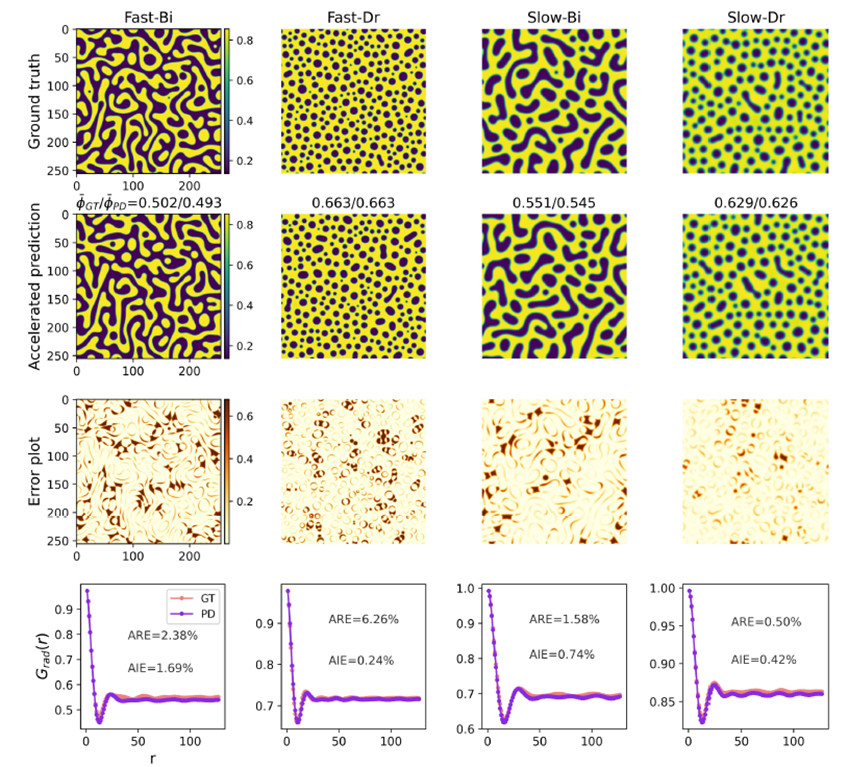
圖四、純數值求解與混合方法之預測結果比較。
表一 純數值解與Hybrid方法之計算時間比較(單位為秒)